Mathématiques - Intégration / Primitives / Convolution
INTEGRATION - PRIMITIVES - CONVOLUTION
1. Intégration
1.1 Intégrale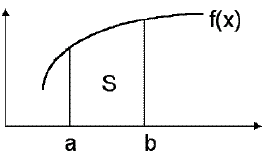
Une intégrale est un nombre, représentant une aire (surface) généralement délimitée par l'axe des abscisses, deux valeurs (éventuellement infinies) sur cet axe et la courbe d'une fonction
y=f(x).
1.2 - Primitives
La primitive F(x) d'une fonction f(x) est telle que
, c'est à dire que sa dérivée est f(x). Elle permet de calculer la surface S de la figure précédente:
2. Distributions
Certains des outils qu'on va voir par la suite s'appliquent non pas à des fonctions, mais à des distributions. En fait cette "nuance" ne nous gênera pas trop, peu de chose étant "démontré mathématiquement".
Retenez juste qu'on trouve deux sortes de distributions:
|
les distributions régulières: ce "sont" les fonctions habituelles et elles sont de la forme:
|
|
|
les distributions singulières: la distribution (ou impulsion) de Dirac d (qui vaut 1 à t=0 et 0 ailleurs), le peigne de Dirac (une série d'impulsions de Dirac espacées d'une période T), l'impulsion (ou porte) I(t), ...
|
3. Le produit de convolution.
3.1 - Présentation
Soit deux fonctions e(t) et h(t), le produit de convolution est l’opération :
C’est une moyenne de h pondérée par e.
Physiquement, h est l’influence de l’instrument de mesure sur l’observation de e.
Le filtrage d’un signal et l'observation d'un signal au travers un appareil de mesure quelconque (car cette observation est un filtrage …) sont des produits de convolution. Donc, on observe pas e(t), mais s(t).
On a une intégration sur R, donc de -inf à +inf. Un signal, ici e(t), subit un "miroir horizontal" et se "promène" devant l'autre. On mesure en permanence la surface (l'intégrale ...) commune sous les deux courbes.
Par exemple pour deux signaux h(t) et e(t):
Le signal convolué h*e se construit:
Parmi les propriétés du produit de convolution, notons la commutativité: h*e = e*h. Cela tombe bien, car on peut ainsi "promener" celui des deux signaux qui nous arrange le plus (utile lorsqu'un des deux n'est pas borné ...).
L'impulsion de Dirac est l'élément neutre de la convolution: e*d = e.
La Transformée de Fourier
L’opérateur qui permet de calculer le spectre d’un signal continu est la transformée de Fourier :
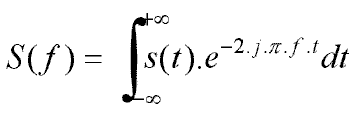
Cet opérateur est réversible, permettant à partir du spectre de retrouver le signal temporel :
Cette propriété peut s'avérer bien pratique pour effectuer un filtrage complexe:
- passage dans le domaine spectral,
- modification du spectre
- retour dans le domaine temporel
ou pour générer un signal complexe:
- description dans le domaine spectral,
- passage dans le domaine temporel.
Si un signal x(t) est une combinaison linéaire de signaux si(t), le spectre X(f) est un combinaison linéaire des spectres Si(f) :
Plus un signal "est large", plus son spectre "est étroit".
A la limite, lorsque a tend vers ¥, 1/a tend vers 0 et le spectre tend donc vers une impulsion de Dirac.
De même, si on considère des portes de plus en plus étroites (a/2, a/4, …) mais de plus en plus haute (2/a, 4/a, …), afin de leur conserver une surface constante égale à 1, les spectres deviennent des sinus cardinaux de plus en plus larges. A la limite, lorsque la porte tend vers une impulsion de Dirac, le spectre tend vers une valeur constante égale à 1.
d (t) ß T.F. à 1
1 ß T.F. à d (f)
Un décalage du signal temporel entraîne une rotation de phase du spectre.
s(t-a) ß T.F. à S(f) e-2ipfa
Une modulation du signal temporel entraîne un décalage en fréquence du spectre.
s(t).e2pft ß T.F. à
S(f-f0)
La transformation de Fourier transforme le produit de convolution en produit simple et le produit en produit de convolution.
s(t)*x(t) ß T.F. à S(f).X(f)
s(t).x(t) ß T.F. à S(f)*X(f)
La Transformée de Fourier discrète
Il en existe une version discrète de la transformée de Fourier (TFD), permettant de travailler sur des signaux échantillonnés:
avec x(n) l’échantillon temporel, X(k) l’échantillon fréquentiel, N le nombre d’échantillons (de points) sur lesquels la transformé est calculée.
La TFD présente la particularité de pouvoir se mettre sous une forme matricielle :
avec 
Celle-ci se calcule aisément sur ordinateur par un algorithme de TFR (Transformée de Fourier Rapide, FFT en anglais), comme celui de Cooley-Tuckey (papillon).
Ceci est une FFT sur 8 points : 8 échantillons temporels à droite et donc 8 échantillons fréquentiels à gauche.
Remarquez que l’ordre des échantillons temporels (à droite) est différent de celui des échantillons fréquentiels à gauche. On parle d’entrelacement temporel. Il est possible de conserver les échantillons temporels dans l’ordre, les échantillons fréquentiel étant alors «mélangés» : c’est l’entrelacement fréquentiel. Pour trouver l'ordre d'entrelacement, écrivez les indices en binaire en intervertissant le sens d'écriture des bits. Dans l'exemple ci-dessus, les 8 échantillons sont indicés de 0 (000) à 7 (111). L'échantillon à la 7ème place (indice 6: 110) est celui indicé 3 (011).
Remarquez également la structure récursive de l'algorithme: calculer une FFT sur 8 points revient à en calculer 2 sur 4 points, chacune de ces deux revenant à en calculer 2 sur 2 points ... Voilà pourquoi le nombre de point doit être une puissance de 2. Dans le cas contraire, vous ne pouvez pas utiliser cet algorithme de FFT et vous devez alors calculer une TFD et c'est nettement plus long!
Si la TFD conserve les propriétés de la TF, elle présente quelques particularités :
- Le nombre d’échantillons fréquentiel (X0 ... XN-1) est le même que le nombre d’échantillons temporels (x0 ... xN-1).
- Les échantillons (X0 ... XN-1) sont répartis linéairement entre 0Hz et fe la fréquence d’échantillonnage.
- La FFT se comporte comme un banc de N filtres RII (Réponse Impulsionnelle Infinie) en parallèles.
- Le prélèvement du signal temporel se fait par une fenêtre, ce qui revient à une multiplication. En application du
théorème de Plancherel, cela entraîne, dans le domaine fréquentiel, une convolution du spectre du signal par le
spectre de la fenêtre.
- Le passage dans le domaine spectral fait perdre les informations temporelles : on sait dans quelle fenêtre s’est
produit l’événement, mais pas à quel instant.
- Le fait de travailler sur un signal échantillonné, périodise le spectre tous les fe , d'où la nécessité de prévoir un filtre
anti-repliement.