Mathématiques - Transformée par Ondelettes/Bandelettes, Gabor
1. Rappels :
Le SIGNAL :
La représentation habituelle d'un signal se fait en temps/amplitude
Le SPECTRE :
C'est la représentation d'un signal en fréqence/amplitude
(Onl'obtient grâce à la Transformée de Fourier du signal de départ.)
Le SPECTROGRAMME :
C'est la représentation d'un signal en temps/fréqence/amplitude
(c'est aussi un Spectre auquel on ajoute le paramètre temporel)
exemple :

Signal
Amplitude (y) temps(x)
Spectrogramme
Fréquence (y) temps (x)
amplitude (couleur)
2. - L'étude des fréquences est permise par :
-La transformée de Fourier
-La transformée de Fourier fenêtrée
Une meilleur résolution est obtenue par
-La transformée en ondelettes continue
-La transformée en ondelettes discrète
2.1 - Exemple d'une onde stationnaire :
Prenons un exemple avec un signal simple continu à 50Hz par exemple/
Remprésentation Amplitude/Temps
Cette représentation nous montre que le signal est continu, qu'il a une amplitude comprise entre -1 et 1. On voit bient à vue d'oeil que c'est un signal périodique à une certaine fréquence, mais il nous est imossible d'en déterminer la fréqence exacte à l'oeil nu.
Si on y applique une transformée de Fourier, on va afficher ce signal en fréquence, par contre, nous perdrons la notion de temps :
Représentation Amplitude/Fréquence (spectre)
On voit sur ce graphique se détacher nettement une fréquence particulière à 50 Hz (le pic)
remarque : le temps n'y est plus représenté (Amplitude sur l'axe des ordonnées y )
mathématiquement cela nous donne :
soit x : un signal temporel, X un signal dans le domaine fréquentiel
t : temps et f : fréquence
Transformée de FOURIER (FT)
Transformée de FOURIER inverse (FT-1)
Formules des Transformée et Transformée inverse de Fourier
exemple sur un signal stationnaire à plusieurs composantes (fréquences)

Transformée d'un signal complexe composé de quatres fréquences diférentes
La transformée de Fourier permet de décomposer efficacement le signal complexe en une suite de fréquences
(Un signal complexe est la somme de plusieurs signaux simples de fréquences différentes)
Limites de la Transformée de Fourier :
Elle n'est efficace que sur les signaux stationnaires (signaux dont le contenu en fréquence ne change pas au cours du temps)
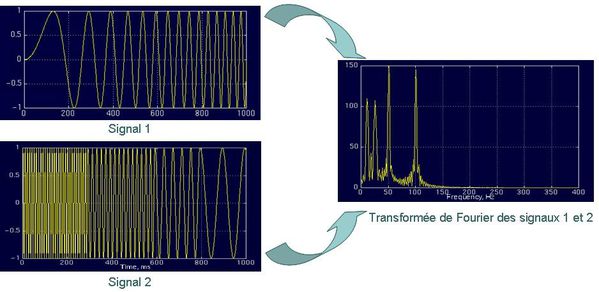
Transformée de Fourier de deux signaux non stationnaires différents
Dans l'exemple de la figure cidessus, nous avons deux signaux NON STATIONAIRES, la transformé de Fourier nous donne une représentation unique alors que les deux signaux sont complètements différents !
Pour remédier à ce problème, il faut conserver l'information du temps : il faut passer à la Transformée de Fourier fenêtrée. Cette dernière tiens compte de la variation de la fréquence de cette onde dans le temps
2.2. - Cas des ondes non stationnaire :
2.2.1 La Transformée de Fourier fenêtrée :
La transformée de Fourier fenêtrée consiste à appliquer la TF pour chaque morceau du signal contenu dans la fenêtre et décaler la fenêtre tout le long du signal.
 Transformée fenêtrée d'un signal non stationnaire
Transformée fenêtrée d'un signal non stationnaire

Voilà à quoi ressemble graphiquement ( spectre en trois dimentions temps, fréquence, amplitude) une transformée de Fourier fenêtrée :
Grâce à cette représentation tri dimentionnelle de la Transformée Fenêtrée de Fourier, chaque fenêtre correspond à une "montagne"
On peut dire en voyant ce spectre 3D que le signal de base non stationnaire évolue selons quatres états distincts.
On peut d'ailleur presque imaginer l'effet sonore en voyant cette représentation :
il doit s'agire de deux sons mélangés convergant vers les 125Hz (l'un monte partant de 30Hz vers 125Hz et l'autre descend vers les 125Hz en partant de 250Hz).
On peut constater malgré tout un problème de résolution au niveau du fenêtrage :On a l'impression d'une discontinuité des différentes plages de signaux (alors qu'en réalité iln'en est rien).
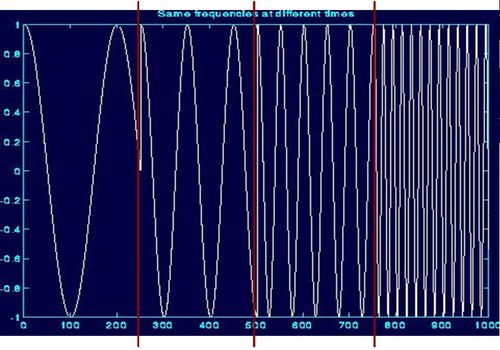
Il faut choisir une fenêtre suffisament étroite pour considérer chaque signal stationnaire en tenant compte du fait que :
1) Plus la fenêtre est étroite / plus la résolution en temps et bonne mais plus la résolution en fréquence est mauvaise
2) Plus la fenêtre est large / plus la résolution en temps est mauvaise mais plus la résolution en fréquence est bonne
Illustration de cette problématique :
Variation de la taille du fenêtrage Résultats obtenus
La résolution n° 4 permet une lecture plus juste du signal non stationnaire :
Transformée de Fourier Fenêtrée d'un signal complexe non stationnaire
3. La Transformée en Ondelettes
La Transformée en ondelettes est basée sur le même principe que la Transformée Fenêtrée de Fourier.
La différence énorme est la fait que l'on utilise une fenêtre dont la largeure est variable.
Ceci nous permet de résoudre un problème de résolution lié aux type de fréquences. Nous pourrons obtenir plus de précisions dans les résultats selon si il s'agit de fréquences basses ou hautes.
Mathématiquement, cela nous donne ;
L'idée générale qui se dégage des ondelettes est d'étudier le signal avec des échelles différentes :
des fenêtres étroites pour les hautes fréquences (bonne résol. temps mais moins bonne en Fq)
des fenêtres larges pour les basses fréquences (bonne résol. en Fq mais mais moins bonne en temps)
3.1 L'Ondelette mère et son échelle
Grâce au coéficient d'échelle on obtient des versions différentes (dilatées ou compressées) de fenêtre à partir d'une même ondelette mère.
Ondelette mère de HARR :
Ondelette de HAAR
L'ondelette de HAAR est la plus simple des ondelettes mère. Elle offre une très bonne détection des contours, cependant l'amortissement très long dans le domaine fréquentiel confère à ces contours une très mauvaise résolution fréquentielle.
Ondelette mère de MORLET
Ondelette de MORLET
exemples de déformation de l'ondelette mède de MORLET après compression ou dilitation (avec l'utilisation du coeficient)
Ondelettes de DEBAUCHIES :
Ces ondelettes proposées à la fin des années 80 par Ingrid DAUBECHIES offrent à la fois de très bonnes représentations spatiales et fréquentielles.
Principe de découpage :
Nous allons utiliser des fenêtres de largeur différentes en fonction des fréquences
(étroite pour les hautes fréquences et larges pour les basses fréquences)
voici comment on peut se représenter ce découpage :

3.2 Etapes de la Transformée de Fourier en Ondelettes
1 - Choix du type d'ondelette mère
2 - Initialisation de l'échelle et du paramètre de décalage
3 - Etude des fréquences de la portion de signal contenue dans la fenêtre (ondelette mère) qui correspond à l'échelle
4 - Décalage de l'ondelette de long du signal par rapport à "téta"
5 - Choix d'une nouvelle valeur pour l'échelle
Représentation Graphique du processus (sens de lecture / Gà D et H vers B)


Dans les figures ci dessous, si S (la largeur de la fenêtre) est faible, le résultat sera élevé autour de 100ms uniquement.
Si S (la largeure de la fenêtre) est élevée, alors le résultat sera élevé sur presque tout le signal (car il est composé de beaucoup de basses fréquences).
3.3 La Transformée de Fourier en Ondelettes Discrète
On va grâce à elle discrétiser le signal :
On sépare le signal en deux composantes représentant :
1 - Les basses fréquences / ce qui correspond à l'allure générale du signal : APPROXIMATION
2 - Les hautes fréquences / qui correspondent aux détails du signal : DETAILS
Pour réaliser ce découpage, nous utiliserons des filtres Passe-bas et Passe Haut.
Rappel :
un filtre passe-bas est un filtre qui supprime les hautes fréquence à partir d'une fréquence donnée.
un filtre passe-haut fait l'inverse : il supprime les fréquences basses pour ne laisser passer que les fréquences élevées.
schéma de principe :
Discrétisation du signal (découpage)
Les Filtres passe-haut et passe-bas sont en fait des ondelettes avec une échelle adaptée aux fréquences à récupérer
Il suffit de bien choisir l'échelle / Un filtre agit comme l'ondelette mère du signal
On obtient alors deux signaux de longeur N/2, si la longueur du signal d'origine est N puisque cela revient à procéder à un sous échantillonnage (on aura deux fois moins de points par rapport à l'échantillon du signal complet)
On procède ensuite à n répétitions de l'opérations ce qui revient à étudier le même signal au travers de plusieurs résolutions différentes :

Le traitement par ondelette d'une image bruitée donnerait ceci :
image source bruitée Décomposition en ondelette 1er rang
La première ittération de la décomposition de l'image source (Lena) permet de voir l'effet produit par cet outils. L'image en clair en haut à droite correspond à l'Approximation, et les trois autres aux Détails.
On voit clairement que le signal détail ne contient pas d'information significative.
A notter également, l'image complète de Léna existe sur le net, elle mériterait de figurer également dans les études :).
(je ne mettrai pas le lien sur mon blog).
4. La Transformée en Ondelettes Inverse
Onprocède selon un chemin inverse par rapport à la Transformée en Ondelettes :
Nous allons reconstruire le signal à parir des coefficients d'ondelettes
Les coefficients d'ondelettes sont : APPROXIMATION+DETAILS
remarque : Seule la dernière approximation suffit pour faire une bonne reconstruction car
A(n) = A(n+1) + D(n+1)
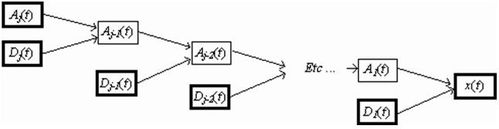
Schéma de la Transformé de Fourier en Ondelettes Inverse
5. La Transformée en Ondelette de GABOR (ou filtres de Gabor)
Considérons la transformée de Fourier suivante :
et choisissons la faonction gaussienne que l'onfera glisser sur le signal :
On peut observer que plus la fenêtre choisie est étroite et plus on pourra localiser précisément les pics à t0 et t1
Cette nouvelle tchnologie peut être appliquée dans de multiples domaines.
Voir également mon autre blog : outilsrecherche sur over-blog.com
